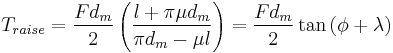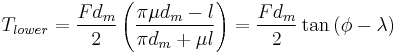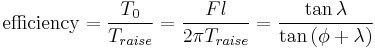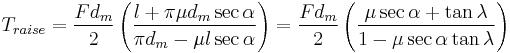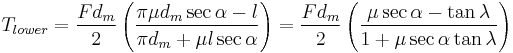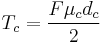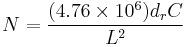Leadscrew
A leadscrew (or lead screw), also known as a power screw[1] or translation screw,[2] is a screw designed to translate turning motion into linear motion. Common applications are machine slides (such as in machine tools), vises, presses, and jacks.[3]
Leadscrews are manufactured in the same way as other thread forms.
A lead screw can be used in conjunction with a split nut.
Contents |
Types
Power screws are classified by the geometry of their thread. V-threads are less suitable for leadscrews than others such as Acme because they have more friction between the threads. Their threads are designed to induce this friction to keep the fastener from loosening. Leadscrews, on the other hand, are designed to minimize friction.[4] Therefore, in most commercial and industrial use, V-threads are avoided for leadscrew use. Nevertheless, V-threads are sometimes successfully used as leadscrews, for example on microlathes and micromills.[5]
Square thread
Square threads are named after their square geometry. They are the most efficient, having the least friction, so they are often used for screws that carry high power. But they are also the most difficult to machine, and are thus the most expensive.
Acme thread
Acme threads have a 29° thread angle, which is easier to machine than square threads. They are not as efficient as square threads, due to the increased friction induced by the thread angle.[3]
Buttress thread
Buttress threads are of a triangular shape. These are used where the load force on the screw is only applied in one direction.[6] They are as efficient as square threads in these applications, but are easier to manufacture.
Characteristics
A leadscrew nut and screw mate with rubbing surfaces, and consequently they have a relatively high friction and stiction compared to mechanical parts which mate with rolling surfaces and bearings. Leadscrew efficiency is typically between 25 and 70%, with higher pitch screws tending to be more efficient. A higher performing but more expensive alternative is the ball screw.
The high internal friction means that leadscrew systems are not usually capable of continuous operation at high speed, as they will overheat. Due to inherently high stiction, the typical screw is self-locking (i.e. when stopped, a linear force on the nut will not apply a torque to the screw) and are often used in applications where backdriving is unacceptable, like holding vertical loads or in hand cranked machine tools.
Leadscrews are typically used well greased, but, with an appropriate nut, they may be run dry with somewhat higher friction. There is often a choice of nuts, and manufacturers will specify screw and nut combination as a set.
The mechanical advantage of a leadscrew is determined by the screw pitch and lead. For multi-start screws the mechanical advantage is lower, but the traveling speed is higher.[7]
Backlash can be reduced with the use of a second nut, or a tensioning spring, to create a static loading force known as preload; alternately, the nut can be cut across its diameter and preloaded by clamping that cut back together.
A leadscrew with a sufficiently high helix angle can back drive: forces on the nut applied parallel to such a leadscrew will cause the leadscrew, if it is not otherwise held in place, to rotate. Such a tendency to backdrive depends on the thread helix angle, coefficient of friction of the interface of the components (screw/nut) and the included angle of the thread form. In general, a steel acme thread and bronze nut will back drive when the helix angle of the thread is greater than 20°.
Advantages & disadvantages
The advantages of a leadscrew are:[2]
- Large load carrying capability
- Compact
- Simple to design
- Easy to manufacture; no specialized machinery is required
- Large mechanical advantage
- Precise and accurate linear motion
- Smooth, quiet, and low maintenance
- Minimal number of parts
- Most are self-locking
The disadvantages are that most are not very efficient. Due to the low efficiency they cannot be used in continuous power transmission applications. They also have a high degree for friction on the threads, which can wear the threads out quickly. For square threads, the nut must be replaced; for trapezoidal threads, a split nut may be used to compensate for the wear.[4]
Alternatives
Alternatives to actuation by leadscrew include:
- Ball screws and roller screws (sometimes categorized as types of leadscrew rather than in contradistinction)
- Fluid power (i.e., hydraulics and pneumatics)
- Gear trains (e.g., worm drives, rack-and-pinion drives)
- Electromagnetic actuation (e.g., solenoids)
- Piezoelectric actuation
Mechanics
The torque required to lift or lower a load can be calculated by "unwrapping" one revolution of a thread. This is most easily described for a square or buttress thread as the thread angle is 0 and has no bearing on the calculations. The unwrapped thread forms a right angle triangle where the base is 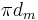 long and the height is the lead (pictured to the right). The force of the load is directed downward, the normal force is perpendicular to the hypotenuse of the triangle, the frictional force is directed in the opposite direction of the direction of motion (perpendicular to the normal force or along the hypotenuse), and an imaginary "effort" force is acting horizontally in the direction opposite the direction of the frictional force. Using this free-body diagram the torque required to lift or lower a load can be calculated:[8][9]
long and the height is the lead (pictured to the right). The force of the load is directed downward, the normal force is perpendicular to the hypotenuse of the triangle, the frictional force is directed in the opposite direction of the direction of motion (perpendicular to the normal force or along the hypotenuse), and an imaginary "effort" force is acting horizontally in the direction opposite the direction of the frictional force. Using this free-body diagram the torque required to lift or lower a load can be calculated:[8][9]
| Screw material | Nut material | |||
|---|---|---|---|---|
| Steel | Bronze | Brass | Cast iron | |
| Steel, dry | 0.15–0.25 | 0.15–0.23 | 0.15–0.19 | 0.15–0.25 |
| Steel, machine oil | 0.11–0.17 | 0.10–0.16 | 0.10–0.15 | 0.11–0.17 |
| Bronze | 0.08–0.12 | 0.04–0.06 | - | 0.06–0.09 |
where
- T = torque
- F = load on the screw
- dm = mean diameter
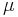 = coefficient of friction (common values are found in the table to the right)
= coefficient of friction (common values are found in the table to the right)- l = lead
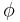 = friction angle
= friction angle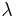 = lead angle
= lead angle
Based on the Tlower equation it can be found that the screw is self-locking when the coefficient of friction is greater than the tangent of the lead angle. An equivalent comparison is when the friction angle is greater than the lead angle (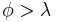 ).[11] When this is not true the screw will back-drive, or lower under the weight of the load.[8]
).[11] When this is not true the screw will back-drive, or lower under the weight of the load.[8]
The efficiency, calculated using the torque equations above, is:[12][13]
For screws that have a thread angle other than zero, such as a trapezoidal thread, this must be compensated as it increases the frictional forces. The equations below takes this into account:[12][14]
where 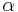 is one half the thread angle.
is one half the thread angle.
If the leadscrew has a collar in which the load rides on then the frictional forces between the interface must be accounted for in the torque calculations as well. For the following equation the load is assumed to be concentrated at the mean collar diameter (dc):[12]
where 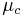 is the coefficient of friction between the collar on the load and dc is the mean collar diameter. For collars that use thrust bearings the frictional loss is negligible and the above equation can be ignored.[15]
is the coefficient of friction between the collar on the load and dc is the mean collar diameter. For collars that use thrust bearings the frictional loss is negligible and the above equation can be ignored.[15]
| Material combination | Starting 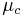 |
Running 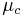 |
|---|---|---|
| Soft steel / cast iron | 0.17 | 0.12 |
| Hardened steel / cast iron | 0.15 | 0.09 |
| Soft steel / bronze | 0.10 | 0.08 |
| Hardened steel / bronze | 0.08 | 0.06 |
Running speed
| Nut material | Safe loads [psi] | Speed |
|---|---|---|
| Bronze | 2500–3500 | Low speed |
| Bronze | 1600–2500 | 10 fpm |
| Cast iron | 1800–2500 | 8 fpm |
| Bronze | 800–1400 | 20–40 fpm |
| Cast iron | 600–1000 | 20–40 fpm |
| Bronze | 150–240 | 50 fpm |
The running speed for a leadscrew (or ball screw) is typically limited to, at most, 80% of the calculated critical speed. The critical speed is the speed that excites the natural frequency of the screw. For a steel leadscrew or steel ballscrew, the critical speed is approximately[17]
where
- N = critical speed in RPM
- dc = smallest (root) diameter of the leadscrew in inches
- L = length between bearing supports in inches
- C = .36 for one end fixed, one end free
- C = 1.00 for both ends simple
- C = 1.47 for one end fixed, one end simple
- C = 2.23 for both ends fixed
See also
References
- ^ Ball Screws & Lead screws, http://www.thomsonbsa.com/, retrieved 2008-12-16.
- ^ a b Bhandari, p. 202.
- ^ a b Shigley, p. 400.
- ^ a b Bhandari, p. 203.
- ^ Martin 2004, p. 266.
- ^ Bhandari, p. 204.
- ^ Bhandari, pp. 205–206.
- ^ a b Shigley, p. 402.
- ^ Bhandari, pp. 207–208.
- ^ Shigley, p. 408.
- ^ Bhandari, p. 208.
- ^ a b c Shigley, p. 403.
- ^ Bhandari, p. 209.
- ^ Bhandari, pp. 211–212.
- ^ a b Bhandari, p. 213.
- ^ Shigley, p. 407.
- ^ Nook Industries, Inc. "Acme & lead screw assembly glossary and technical data"
Bibliography
- Bhandari, V B (2007), Design of Machine Elements, Tata McGraw-Hill, ISBN 9780070611412, http://books.google.com/?id=f5Eit2FZe_cC.
- Martin, Joe (2004), Tabletop Machining: A Basic Approach to Making Small Parts on Miniature Machine Tools, Vista, California, USA: Sherline, Inc., ISBN 978-0-9665433-0-8. Originally published in 1998; content updated with each print run, similar to a "revised edition". Currently in the fourth print run.
- Shigley, Joseph E.; Mischke, Charles R.; Budynas, Richard Gordon (2003), Mechanical Engineering Design (7th ed.), McGraw Hill, ISBN 9780072520361, http://books.google.com/?id=j8xscqTxWUgC.
External links
|
||||||||||||||||||||